Spherical Trigonometry
One of the primary concerns in astronomy throughout history was the positioning of the heavenly bodies, for which spherical trigonometry was required. The diagrams below show trihedrals, polyhedra with triangular sides. For astronomy, V is the position of the observer, and PQR are points on a sphere centred at V, the celestial sphere.
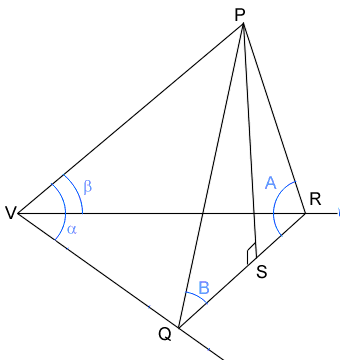
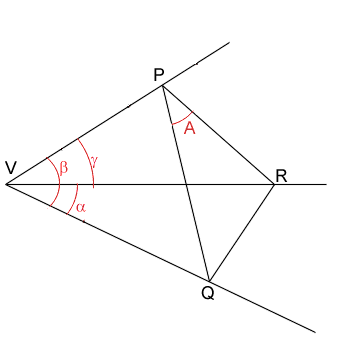
From 2 dimensional trigonometric relations the upper diagram gives:
Simplifying and applying Pythagoras' Theorem gives:
Which can be simplified further, dividing by (VQ)(VR) using 2 dimensional trigonometrical relations to give the first law of cosines for trihedrals:
Construction of a second trihedral called the polar trihedral from the first gives a different set of relationships between the quantities of the first law, the second law of cosines:
These equations can be used to calculate positions on the celestial sphere, however, the laws can be simplified by consideration of the spherical triangle (see diagram below).
The spherical triangle in the diagram above is the same as the trihedral, except that the sides a, b and c are great circle paths on the surface of the sphere centred at V rather than straight lines (as in the trihedral).
Since a = (VC) 2 π α / 360
b = (VA) 2 π β / 360
c = (VB) 2 π γ / 360
and VC=VB=VA since they are all radii of the sphere, then the law of sines for trihedrals becomes (cancelling 2 (VC) π / 360 as a common multiplier):
this is the law of sines for spherical triangles.
Similar substitutions convert the first law of cosines for trihedrals into the law of cosines for the sides of spherical triangles:
And the second law of cosines becomes a law of cosines for the angles of spherical triangles:
To solve a spherical triangle problem, known values are substituted into the equations, which are then solved for the remaining unknown values. This enables great circle distances between points on the celestial sphere to be calculated from angles between them, and other similar calculations. These equations are clearly not simple or easy to solve, so a great deal of time and effort was put into simplifying the necessary calculations for astronomers. One of the most important and effective methods of simplification was the use of logarithms, which can convert problems of multiplication into problems of addition and back again. This simplification enabled them to eradicate caculatory errors.
PS = QP sin B = VP sin α sin B = RP sin A = VP sin β sin A
Other, similar relations can be derived, and then simplified to give the law of sines for trihedrals:
(sin α)/sin A =
QR2 = PQ2 + PR2 - 2PQ PR cos A = VQ2 + VR2 - 2 VQ VR cos a
2 VQ VR cos α = 2 VP2 + 2 PQ PR cos A
cos α = cos β cos γ + sin β sin γ cos A
cos A = -cos B cos C + sin B sin C cos α
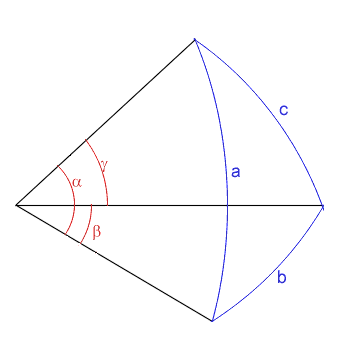
(sin a)/(sin A) = (sin b)/(sin B) = (sin c)/(sin C)
cos a = cos b cos c + sin b sin c cos A
cos A = -cos B cos C + sin B sin C cos a