Mathematical Techniques: The Celestial Sphere
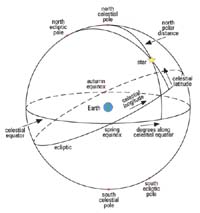Diagram of the celestial sphere.
The concept of the celestial sphere was fundamental to positional astronomy throughout Antiquity, the Middle Ages, and the Early-Modern era, and still remains useful today. In essence, the celestial sphere discussed here is a geometric model, but in former times the concept of a physical sphere or spheres was also basic to much cosmological discussion. Many authors stressed the importance of a clear distinction between the two, particularly as part of the demarcation of mathematical astronomy from natural philosophy. In practice, however, this distinction was often difficult to maintain.
The diagram below represents the celestial sphere. At the centre of the sphere is the Earth, and hence the observer's vantage point. The surface of the sphere acts as the reference against which all celestial bodies observed from the centre are located. Since, from the geocentric perspective, the heavens appear to rotate around the earth once every twenty-four hours, the celestial sphere is considered to possess this particular motion. The axis of rotation terminates in the north and south celestial poles; equidistant between the poles, the sphere is encircled by the celestial equator. At a fixed angle to the equator is another great circle of the celestial sphere, the ecliptic. This represents the annual path of the sun. The two points when the ecliptic and equator cross therefore mark the position of the sun at the spring (vernal) and autumn equinoxes.
The position of any point on the surface of the sphere (and hence that of any celestial body which is referred to it) can be given with reference to the equator or the ecliptic. In the equatorial co-ordinate system, position is specified by right ascension and declination. Right ascension is the angular distance along the equator from the vernal equinox; declination is the distance north or south of the equator along a great circle passing through the point in question and the two celestial poles. In the ecliptic co-ordinate system, position is specified by celestial longitude and latitude. Celestial longitude is the angular distance along the ecliptic, again from the vernal equinox; celestial latitude is the distance north or south of the ecliptic along a great circle passing through the two celestial poles.
Another co-ordinate system used by astronomers is the horizontal system, in which bodies are located according to their altitude and azimuth. The altitude of a body is its angular distance north or south of the horizon; a body has an altitude of 90° when it is at the observer's zenith. The azimuth is the angular distance along the horizon from the northernmost point. However, since the horizon of an observer varies with his or her terrestrial latitude, the horizontal system is a strictly local co-ordinate system. Instruments such as armillary spheres and celestial globes, which represent the celestial sphere, therefore have to be set to the appropriate latitude, if possible, when the horizontal system is employed.
Accounts of the celestial sphere typically refer to other circles on its surface, including the arctic and antarctic circles, the zodiac, tropics, and the solstitial and equinoctial colures. The zodiac is a band which extends to either side of the ecliptic, and is divided into the twelve zodiacal signs; it contains the courses of all the planets known to the Ancients. The Tropic of Cancer is a circle parallel to the celestial equator which touches the ecliptic at its northernmost point; when the sun is at this point, just about to enter the zodiacal sign of Cancer, it is the summer solstice. The Tropic of Capricorn holds the same position with respect to the point on the ecliptic corresponding to the winter solstice. The solstitial colure is a great circle which passes through the celestial poles and these two solstitial points. The equinoctial colure is a great circle which passes through the celestial poles and the ecliptic at the two equinoxes.